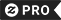Tippe / klicke auf das Bild, um weitere RealViews zu sehenTM
6,09 €
pro Karte
Pythagoräisches Theorem-Beweis unter Verwendung
Anzahl:
Papiersorte
Signature Matt
18 pt Stärke / 120 lb Gewicht. Weichweiße, zarte Eierschalenstruktur.
+0,87 €
+0,87 €
-0,23 €
Über Karten
Verkauft von
Über dieses Design
Pythagoräisches Theorem-Beweis unter Verwendung
Beweis unter Verwendung der ähnlichen Dreiecke
Dieser Beweis basiert auf der Proportionalität der Seiten von zwei ähnlichen Dreiecken d.h. nach der Tatsache, dass das Verhältnis aller möglicher zwei entsprechenden Seiten der ähnlichen Dreiecke das selbe unabhängig davon die Größe der Dreiecke ist.
Lassen Sie ABC ein rechtes Dreieck darstellen, wenn das rechtwinklige an C gelegen, wie gezeigt auf der Zahl. Wir zeichnen die Höhe von Punkt C und nennen H seinen Schnitt mit der Seite AB. Punkt H teilt das Länge der Hypothenuse c in Teile d und E. unter. Das neue Dreieck ACH ist Dreieck ABC, weil sie ähnlich, die beide ein rechtwinkliges (durch Definition der Höhe) haben, und sie teilen den Winkel an A und bedeuten, dass der dritte Winkel der selbe in beiden Dreiecken auch ist, markiert als θ in der Zahl. Durch eine ähnliche Argumentation ist das Dreieck CBH auch ABC ähnlich. Der Beweis der Ähnlichkeit der Dreiecke erfordert das Dreieckpostulat: die Summe der Winkel in einem Dreieck ist zwei Winkel, und ist mit dem parallelen Postulat gleichwertig.
http://en.wikipedia.org/wiki/File:Pythagoras_similar_triangles.svg
Automatische Übersetzung
Kundenrezensionen
4.8 von 5 Sternen Bewertung32 Bewertungen insgesamt
32 Bewertungen
Bewertungen für ähnliche Produkte
5 von 5 Sternen Bewertung
Von A.29. Dezember 2017 • Geprüfter Kauf
Gefaltete Karte, Größe: Standard (12,7 cm x 17,8 cm), Papier: Signature Matt
Bewertungsprogramm bei Zazzle
Eine sehr schöne Karte genau so wie ich es mir vorgestellt habe. Der Druck war hervorragend und genau so wie ich es wollte
5 von 5 Sternen Bewertung
Von M.17. August 2021 • Geprüfter Kauf
Gefaltete Karte, Größe: Standard (12,7 cm x 17,8 cm), Papier: Signature Matt
Bewertungsprogramm bei Zazzle
Eine sehr schöne Karte und ein toller Kundendienst. Das Motiv und die Farben der Karte ,sowie der Druck sind sehr hochwertig. Genau wie auf der Abbildung. Bin sehr zufrieden.
5 von 5 Sternen Bewertung
Von Jörg M.9. Juni 2018 • Geprüfter Kauf
Gefaltete Karte, Größe: Standard (12,7 cm x 17,8 cm), Papier: Signature Matt
Bewertungsprogramm bei Zazzle
Tolle Postkarte. Schöne ausführung. Tolle Farben. Gelungene Umsetzung
Tags
Andere Informationen
Produkt ID: 137683950939446802
Gemacht am: 3.4.2012, 17:42
Bewertung: G
Zuletzt angesehene Produkte