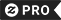Über Tassen
Verkauft von
Über dieses Design
Omega-Punkt Multiverse Diagramm Kaffeetasse
In der hyperbolischen Geometrie wird ein idealer Punkt auch ein Omega-Punkt genannt. Eine Linie L und einen Punkt P nicht auf L, werden Recht- und verlassene-Begrenzungähnlichkeiten zu L bis P gegeben gesagt, um L an Omega-Punkten zu treffen. Anders als den projektiven Fall zeigt Omega Form eine Grenze, nicht ein submanifold. So schneiden diese Linien nicht an einem Omega-Punkt und solche Punkte, obgleich gut definiert, gehören nicht einem hyperbolischen Raum selbst. Im Poincaré Scheibenmodell und im Klein Modell der hyperbolischen Geometrie, können die Omega-Punkte sichtbar gemacht werden, da sie auf dem Grenzkreis liegen (der nicht Teil des Modells ist-). Paschs Axiom und das Außenwinkeltheorem halten noch für ein Omega-Dreieck, definiert um zwei Punkte im hyperbolischen Raum und in einem Omega-Punkt.
Automatische Übersetzung
Kundenrezensionen
4.7 von 5 Sternen Bewertung167 Bewertungen insgesamt
167 Bewertungen
Bewertungen für ähnliche Produkte
5 von 5 Sternen Bewertung
Von J.19. Dezember 2021 • Geprüfter Kauf
Klassische, weiße Tasse, 325 ml
Bewertungsprogramm bei Zazzle
Perfekte Ausführung, entspricht genau dem Muster auf der Website, was nicht immer eine Selbstverständlichkeit ist. Alles sehr genau, keine verschmierten Buchstaben, keine Ungenauigkeiten. Bin sehr zufrieden.
5 von 5 Sternen Bewertung
Von Evi S.2. Januar 2022 • Geprüfter Kauf
Klassische, weiße Tasse, 443 ml
Bewertungsprogramm bei Zazzle
Die Tasse ist sehr praktisch und vielseitig gut zu gebrauchen. Vor allem ist es ein sehr persönliches Geschenk und eine schöne Erinnerung. Die Bilder habe ich selber platzieren können und der Druck ist hervorragend geworden. Genau wie ich es mir gewünscht habe.
5 von 5 Sternen Bewertung
Von Anonym3. August 2025 • Geprüfter Kauf
Klassische, weiße Tasse, 443 ml
Schnelle Lieferung
Schöne Tasse geworden .
Tags
Andere Informationen
Produkt ID: 168955857717366633
Gemacht am: 10.4.2013, 17:15
Bewertung: G
Zuletzt angesehene Produkte