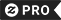Über Tassen
Verkauft von
Über dieses Design
Coprime Gitter von 4 und von 9 Kaffeetasse
Dieses Gitter veranschaulicht, dass die ganzen Zahlen 4 und 9 wenn coprime sind und nur wenn der Punkt mit Koordinaten (4, 9) in einem kartesischen beigeordneten System ist vom Ursprung (0,0), in der Richtung "sichtbar" dass es keinen Punkt mit ganzer Zahl koordiniert zwischen dem Ursprung gibt und (4, 9). In der Mathematik sollen zwei ganze Zahlen a und b coprime oder verhältnismäßig Haupt, wenn sie nicht allgemeinen positiven Faktor anders als 1 haben, oder gleichwertig wenn ihr bestster gemeinsamer Teiler 1. zum Beispiel ist, 6 und 35 coprime sind, aber 6 und 27 nicht coprime sind, weil sie durch 3. beides teilbares sind. Die Nr. 1 ist zu jeder ganzen Zahl coprime. Eine schnelle Weise, zu bestimmen, ob zwei Zahlen coprime sind, wird durch den euklidischen Algorithmus gegeben. Eulers totient Funktion (oder Eulers Phifunktion) einer positiven ganzen Zahl n ist die Zahl ganzen Zahlen zwischen 1 und n, die zu N. coprime sind.
Automatische Übersetzung
Store
Kundenrezensionen
4.7 von 5 Sternen Bewertung167 Bewertungen insgesamt
167 Bewertungen
Bewertungen für ähnliche Produkte
5 von 5 Sternen Bewertung
Von J.19. Dezember 2021 • Geprüfter Kauf
Klassische, weiße Tasse, 325 ml
Bewertungsprogramm bei Zazzle
Perfekte Ausführung, entspricht genau dem Muster auf der Website, was nicht immer eine Selbstverständlichkeit ist. Alles sehr genau, keine verschmierten Buchstaben, keine Ungenauigkeiten. Bin sehr zufrieden.
5 von 5 Sternen Bewertung
Von Evi S.2. Januar 2022 • Geprüfter Kauf
Klassische, weiße Tasse, 443 ml
Bewertungsprogramm bei Zazzle
Die Tasse ist sehr praktisch und vielseitig gut zu gebrauchen. Vor allem ist es ein sehr persönliches Geschenk und eine schöne Erinnerung. Die Bilder habe ich selber platzieren können und der Druck ist hervorragend geworden. Genau wie ich es mir gewünscht habe.
5 von 5 Sternen Bewertung
Von Anonym3. August 2025 • Geprüfter Kauf
Klassische, weiße Tasse, 443 ml
Schnelle Lieferung
Schöne Tasse geworden .
Tags
Andere Informationen
Produkt ID: 168591666934840323
Gemacht am: 10.9.2009, 7:57
Bewertung: G
Zuletzt angesehene Produkte